Kakuro is the most recent puzzle to be described by the cliché "the latest craze in Japan is now sweeping the UK." It has similarities with sudoku as far as numbers have to be slotted into rows and columns based on which numbers occupy other squares, but there is one significant difference: kakuro does involve some maths.

Take a look at kakuro.info‘s daily puzzle to see what a whole puzzle looks like.

How it works

Given a grid, the aim is to ensure that every block adds up to the number at its beginning, using the digits 1-9 a maximum of once each. The numbers in the grid below indicate that the top row must add up to 4, the second row to 7, the first column must add up to 5, the second column to 3 and the third to 4.

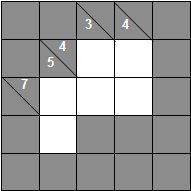
The key with kakuro is to know some of the most common patterns of numbers that add up to certain targets. For example, 3, as in the second column of the grid, can only ever be the total of two digits: 1 and 2. Just knowing this tells us that the second column has a 1 and a 2, but we don’t yet know in which order.

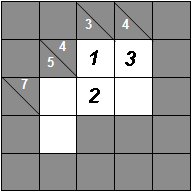
Now look at the first row: two squares which must add to 4. This sum can’t be 2+2 because that would repeat a digit, so the squares must contain a 1 and a 3. The first two intersects with the second column, which we’ve established contains a 1 and a 2, so they must share the 1.

The last column adds up to 4 again, and we know that the top cell has a 3 in it, so the bottom cell must be a 1.

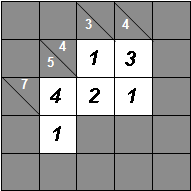
The second row must add up to 7, and we already have a 1 and a 2 so we know the other square must contain a 4. This is a useful one to remember: to make 7 from three cells, the only possibly option is 1+2+4.

Finally, the first column: 5 could be 2+3 or 1+4, but we have the 4 so we can fill in a 1.

Useful numbers
Adding consecutive numbers from 1 upwards or 9 downwards will give the only possible way to build certain numbers. Have a look at these:

1+2 = 3
1+2+3 = 6
1+2+3+4 = 10
1+2+3+4+5 = 15

These are key building blocks of any solution. From these we know that a two-block 3 can only involve a 1 and a 2; a three-block 6t sum must be 1+2+3, etc. They also help us with the next number up if a three-block 6 is 1+2+3, the only possible way to get 7 from three squares is 1+2+4, and the two ways to make 8 are 1+2+5 and 1+3+4.

Equally, we can count down from 9:

9+8 = 17 (the highest possible total from two squares)
9+8+7 = 24 (the highest possible total from three)
9+8+7+6 = 30 (the highest from four)
9+8+7+6+5 = 35 (the highest from five)

Again, by changing the last digit by one we can get the next lower number. So 16 in two squares must be 9+7 and 29 in four squares must be 9+8+7+5.

Now say we have a column of five cells adding to 35 crossing a row of five adding to 15. We know that 35 will be 9+8+7+6+5 and 15 will be 1+2+3+4+5, Only one number appears in both – 5 – and therefore this must fill in the intersecting square.

To find a number up or down from an established sequence, trying varying one of the digits. It won’t be possible to change most without resulting in two identical digits and therefore you can limit the possibilities.

For example, say we want 12 from four digits. 1+2+3+4 is 10 so to reach 12 we need to add 2 (or two 1s). We can’t add 2 to the 1 or the 2 because we already have a 3 and a 4, so we can only add to the 3 and the 4, giving two ways of building 12: 1+2+5+4 and 1+2+3+6.

Other tricks

These basic blocks can be usful elsewhere. Say we have a 27 made of four blocks but we know that one of those is a 3. Subtract the 3 from 27 and we have 24 made from 3 blocks, which we already know must be 9+8+7.

Here are the most important sums to keep in mind.

Two squares:

3 = 1+2
4 = 1+3
16 = 7+9
17 = 8+9

Three squares:

6 = 1+2+3
7 = 1+2+4
23 = 6+8+9
24 = 7+8+9

Four squares:

10 = 1+2+3+4
11 = 1+2+3+5
29 = 9+8+7+5
30 = 9+8+7+6

Five squares:

15 = 1+2+3+4+5
16 = 1+2+3+4+6
34 = 9+8+7+6+4
35 = 9+8+7+6+5

Because these are the highest and lowest totals possible for a given length block, these are the numbers to look for when starting a new puzzle.

With these tips in hand, it should be plain sailing. If you’ve got any other tips to share, or any questions, please pop them in the comments.